ФУНДАМЕНТАЛЬНЫЕ ЗАКОНЫ

Аэродинамика описывается фундаментальными физическими законами механики сплошных сред. Эти законы называются «законами сохранения», так как они выражают свойство сохранения массы, энергии и импульса для каждого элементарного объема движущейся среды.

При использовании законов сохранения важную роль играет принцип относительности движения, сформулированный Галилео Галилеем (1564–1642), согласно которому сила, действующая на тело в воздушном потоке, зависит только от относительной скорости движений тела и воздуха и не зависит от того, движется ли тело в покоящемся воздухе или же воздух движется относительно неподвижного тела.

Применим законы сохранения не к отдельным молекулам, а к некоторому движущемуся элементарному объему среды, содержащему большое число молекул. Этот упрощенный подход представляется неизбежным, если вспомнить, что молекулы, помимо своего перемещения вместе с течением, совершают случайные движения, и законы, описывающие эти движения, должны учитывать столкновения между различными молекулами, в которых изменяются их направления движения, скорости и т.д. Рассмотрим, например, элементарный объем в форме кубика со стороной 0,01 мм, объем которого равен 10^–6 мм³. В этом малом объеме все еще содержится 2,7Ч10¹⁰ молекул, и каждая из них движется случайно. 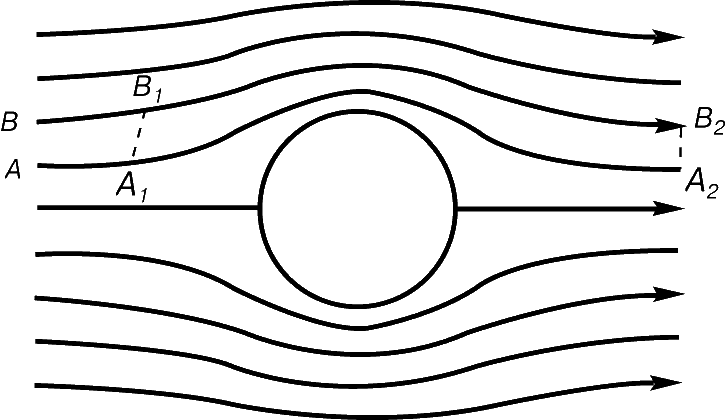Однако вследствие того, что объем содержит большое число молекул, он будет перемещаться со средней скоростью вдоль линий тока течения, изображенных на рис. 2.

Согласно другому условию, этот элементарный объем должен быть настолько мал, чтобы средние скорости в каждой его точке можно было считать приблизительно одинаковыми. Например, если рассматривается обтекание сферы диаметром 10 мм, то элементарный кубик со стороной 0,01 мм будет достаточно малым для того, чтобы он рассматривался как одно целое, перемещающееся вдоль линии тока.

Таким образом, мы рассматриваем элементарный объем среды, который достаточно велик для того, чтобы в нем содержалось большое число молекул, и достаточно мал по сравнению с «характерным масштабом» течения. На очень больших высотах, где плотность воздуха мала, понятие частицы среды теряет смысл, и приходится рассматривать движения отдельных молекул. Линии тока течения определяются как траектории частиц текущей среды. Линии тока могут быть визуализированы с помощью струек дыма, вдуваемого в воздушный поток.

В применении к рассматриваемым частицам текущей среды закон сохранения массы означает, что массовый поток воздуха, проходящего между линиями тока A и B на рис. 2, один и тот же, в каком бы месте он ни измерялся. Следовательно, поток воздуха через линию A₁B₁ такой же, как поток воздуха через линию A₂B₂. Этот закон называется еще уравнением неразрывности, и течение, удовлетворяющее этому условию, называется непрерывным течением.

Закон сохранения импульса является выражением второго закона Ньютона в применении к частицам текущей среды. Он может быть записан в следующей форме:

Сила = Изменение импульса за секунду.

Следствием этого закона является связь между давлением p, плотностью r и скоростью v. Если скорость течения достаточно мала (так что плотность можно считать постоянной всюду в поле течения), то выполняется следующее простое соотношение:

p + ¹/₂ rv² = const.

Эта формула, известная как закон Бернулли, была получена швейцарским математиком и инженером Даниилом Бернулли (1700–1782).

Течение, которое удовлетворяет этому уравнению, называется несжимаемым, поскольку оно применимо как к жидкостям, которые практически несжимаемы, так и к газам, если скорости их движения малы по сравнению со скоростью звука. Если скорость в какой-либо точке потока больше половины скорости звука, то расчеты по этой формуле будут содержать значительные погрешности. Такие течения называются сжимаемыми.

Третий закон сохранения, используемый для описания деталей поля течения, выражает условие сохранения энергии. Применительно к течениям можно рассматривать два рода кинетической энергии: энергию, связанную с основным (упорядоченным) течением, и энергию, соответствующую случайным движениям молекул. Энергию, связанную со структурой отдельных молекул и атомов, мы рассматривать не будем, так как ее влияние становится заметным лишь при очень высоких температурах.

В расчете на единицу объема кинетическая энергия упорядоченного движения записывается как ¹/₂ rv², тогда как кинетическая энергия случайных (неупорядоченных) движений равна rc_pT, где c_p – удельная теплоемкость при постоянном давлении и T – абсолютная температура воздуха. Согласно закону сохранения энергии для установившихся течений, сумма отнесенных к единице объема энергиий упорядоченного и случайного движений сохраняет постоянное значение:

с_рT + ¹/₂ v² = const.

Из этого уравнения энергии видно, что если скорость течения v увеличивается, то его температура T уменьшается.

Параметры течения и движущегося тела.

Силу, действующую на движущееся тело, можно выразить с помощью некоторого безразмерного параметра. Этот параметр получается, если силу отнести к некоторой комбинации существенных характеристик среды и течения, также имеющей размерность силы. По второму закону Ньютона сила F равна произведению массы на ускорение и имеет размерность ml/t ², где m – масса, выраженная в кг, l – длина и t – время (с). Величиной, имеющей размерность силы, является произведение плотности r, квадрата скорости движения тела в среде v² и площади S. Искомый безразмерный параметр, который называется коэффициентом силы, определяется следующим соотношением:

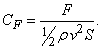
Множитель 1/2 вводится из соображений удобства, так как такой же множитель содержится в уравнении Бернулли, приведенном выше. Сила как векторная величина, характеризуется своими компонентами, имеющими различные направления. Соответственно этому различают три коэффициента сил: коэффициент подъемной силы (нормальной к скорости набегающего потока), коэффициент силы сопротивления (направленной вдоль скорости набегающего потока) и коэффициент боковой силы (ортогональной двум предыдущим).

Сам коэффициент силы зависит от других безразмерных параметров. Одним из них является число Рейнольдса Re, введенное английским инженером Осборном Рейнольдсом (1842–1912). Этот критерий определяется формулой

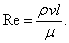
Здесь m – коэффициент вязкости, имеющий размерность m/lt.

Длина l, входящая в определение критерия Рейнольдса, является характерным масштабом течения. Для течения около сферы в качестве l можно взять диаметр сферы, для самолета это хорда крыла, а для трубы – ее диаметр. Это означает, что можно сравнивать числа Рейнольдса для течений различных сред (с различными значениями r и m) около двух сфер или двух геометрически подобных самолетов. Однако не имеет смысла сравнивать числа Рейнольдса течений около сферы и около самолета, так как эти тела не являются геометрически подобными и нельзя определить один масштаб длины, устанавливающий соответствие между этими двумя видами течений. Сопоставление чисел Рейнольдса для течений около двух сфер может служить указанием об относительном влиянии вязкости среды на характер течения.

Вторым определяющим критерием является число Маха M,

M = v/a,

введенное австрийским физиком Эрнстом Махом (1838–1916). Число Маха может служить мерой влияния сжимаемости на аэродинамические характеристики тел.

Излагаемые здесь сведения касаются главным образом влияния чисел Рейнольдса и Маха на аэродинамические характеристики, т.е. на подъемную силу и сопротивление крыльев и других элементов самолета. Ниже будет показано, что каждое из этих чисел определяет некоторые особенности обтекания, соответствующие высоким или низким значениям размера тела, скорости или высоты полета.